Question

A rug cleaning company sells three models. EZ models weighs 10 pounds, packed in a 10-cubic-foot box. Mini model weighs 20 pounds, packed in an 8-cubic-foot box. Hefty model weighs 60 pounds, packed in a 28-cubic-foot box. A delivery van has 296 cubic feet of space and can hold a maximum of 440 pounds. To be fully loaded, how many of each should it carry if the driver wants the maximum number of Hefty models?

Answer 1

To fully load the delivery van while prioritizing the maximum number of Hefty models, it should carry 7 Hefty models and 2 EZ models, which uses all of the weight capacity and 216 cubic feet of space, leaving 80 cubic feet unused due to the weight limit.

Step-by-step explanation:

To maximize the number of Hefty models in the delivery van, we need to consider both the space and the weight constraints of the van. The van can hold a maximum weight of 440 pounds and has 296 cubic feet of space. One Hefty model weighs 60 pounds and occupies 28 cubic feet, meaning the van can carry a maximum of 7 Hefty models (7 models × 60 pounds/model = 420 pounds and 7 models × 28 cubic feet/model = 196 cubic feet). This leaves us with 20 pounds and 100 cubic feet of space to fill with the EZ and Mini models.

Since we want to fill the remaining space and weight as efficiently as possible, the next step is to add EZ models since they are the smallest. The EZ model weighs 10 pounds and occupies 10 cubic feet, so you can fit 2 EZ models (2 models × 10 pounds/model = 20 pounds and 2 models × 10 cubic feet/model = 20 cubic feet). This fills the weight capacity and uses 20 cubic feet of the remaining space, leaving us with 80 cubic feet of van space unused, but since we have already met the maximum weight limit, we cannot add any more Mini or EZ models without exceeding the weight capacity.

Therefore, to be fully loaded with a priority for the maximum number of Hefty models, the delivery van should carry 7 Hefty models and 2 EZ models, using all of the weight capacity and 216 cubic feet of the available space. Since we cannot add more without exceeding the weight limit, we must leave 80 cubic feet of space unused.

Answer 2

From the information that the question gives us, we have that models:

EZ weights 10 pounds, Box = 10 cubic-foot, represented by letter E

Mini weights 20 pounds, Box = 8 cubic-foot, represented by letter M

Hefty weights 60 pounds, Box = 28 cubic-foot, represented by letter H

The van can hold on a maximum of 440 pounds and has 296 cubic-feet. We have the following equations, to get the optimal solution:

For the weight:

`10E+20M+60H=440`

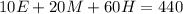
For the volume:

`10E+8M+28H=296`
`\begin{gathered} 10E+20M+60H=440 \\ -(10E+8M+28H)=296 \end{gathered}`

We subtract the two equations to get:

`12M+32H=144`

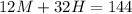
Divide the above equation by 4, to simplify the equation:

`3M+8H=36`

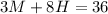
Now we express M in terms of H:

`\begin{gathered} 3M=36-8H \\ M=(36-8H)/(3) \end{gathered}`

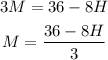
Now we start looking for integer solutions for the above equation, given that we want to maximize H, we can look for integer solutions starting with the largest possible, which is 4. But H=4 does not give an integer solution for M. We can try with H = 3

`\begin{gathered} M=(36-8\cdot3)/(3) \\ M=4 \end{gathered}`

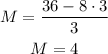
Great, now that we have the number of M (Mini models), we can find the number of Hefty models and EZ models,

For H (Hefty models) we replace M in 3M+8H=36, and solve for H:

`\begin{gathered} 3\cdot4+8H=36 \\ 12+8H=36 \\ 8H=36-12 \\ H=(24)/(8)=3 \end{gathered}`

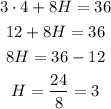
To find E, we can take the first equation 10E+20M+60H=440, to express E in terms of H and M, replace and solve:

`\begin{gathered} 10E+20M+60H=440 \\ 10E=440-20M-60H \\ E=44-2M-6H \\ E=44-2\cdot4-6\cdot3=18 \end{gathered}`

M = 4

H = 3

E = 18