Given:
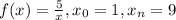
Step-by-step explanation:
To find: The area when n = 2 (since, 2 rectangles)
Finding the given change in x,
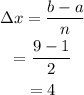
Defining the partition intervals,
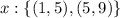
Choose the midpoint in each interval,
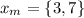
Finding the value of the function at the point,
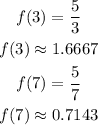
Using the midpoint formula,
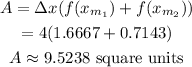
Final answer: The area under 2 rectangles is 9.5238 square units.
To find: The area when n = 4 (4 rectangles)
Finding the given change in x,
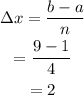
Defining the partition intervals,
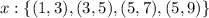
Choose the midpoint in each interval,
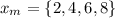
Finding the value of the function at the point,
![\begin{gathered} f(2)=(5)/(2)\Rightarrow f\mleft(2\mright)=2.5 \\ f(4)=(5)/(4)\Rightarrow f\mleft(4\mright)=1.25 \\ f(6)=(5)/(6)\operatorname{\Rightarrow}f(6)=0.8333 \\ f(8=(5)/(8)\operatorname{\Rightarrow}f(8)=0.625 \end{gathered}]()
Using the midpoint formula,
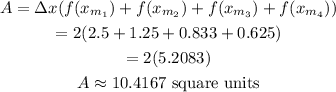
Final answer: The area under 4 rectangles is 10.4167 square units.