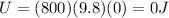Question

1. An 800.0 kg roller coaster car is at rest at the top of a 95 m hill. It rolls down the first drop to a height of 31 m. When it travels to the top of the second hill, it is moving at 28 m/s. It then rolls down the second hill until it is at ground level. Draw a picture of the roller coaster drop and calculate the kinetic and potential energy at the top and bottom of each hill.

Answer:

Answer 1

At the top of first hill

K = 0

U = 744800

At the top of second hill

U = 243040 J

K = 313600 J

At the bottom of the hill

K = 0

Step-by-step explanation:

potential energy is given by

U = mgH

and kinetic energy is given by

`K = (1)/(2)mv^2`

now we have initial potential energy at the top of the hill is given as

`U = (800)(9.8)(95) = 744800 J`

`K = (1)/(2)(800)0 = 0 J`

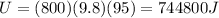
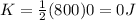
we have initial potential energy at the top of the second hill is given as

`U = (800)(9.8)(31) = 243040 J`

`K = (1)/(2)(800)(28^2) =313600 J`

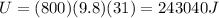
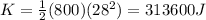
we have initial potential energy at the bottom of the hill is given as

`U = (800)(9.8)(0) = 0 J`

Answer 2

First, we know that the roller coaster is at rest at the top of the first hill, meaning it has no kinetic energy. The formulas are:
Kinetic energy = 1/2 * m * v²
Potential energy = m*g*h
Mechanical energy = potential energy + kinetic energy (mechanical energy remains constant)
Top of first hill:
KE = 0
PE = 800 * 95 * 9.81
PE = 745,560 J
So ME = 745,660
Bottom of first hill:
PE = 800 * 9.81 *31
PE = 243,388 J
KE = 745,660 - 243,388
KE = 502,272

Top of second hill:
KE = 0.5 * 800 * 28²
KE = 313,600 J
PE = 745,660 - 313,600
PE = 432,060 J

Bottom of second hill:
PE = 0 as height is 0
KE = initial PE
KE = 745,660 J