Question

The area of a triangle is 1653. Two of the side lengths are 75 and 46 and the included angle is obtuse. Find the measure of the included angle , to the nearest tenth of a degree.

Answer 1

Missing angle of a triangle

Initial explanation

We have that the area of a triangle is given by

`Area=(1)/(2)ab\sin C`

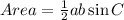
Finding a formula

In this case we have that

a = 75

b = 46

and the area is 1653. We want to find C:

Replacing in the formula, we have:

`\begin{gathered} Area=(1)/(2)ab\sin C \\ \downarrow \\ 1653=(1)/(2)\cdot75\cdot46\cdot\sin C \\ 1653=1725\cdot\sin C \end{gathered}`

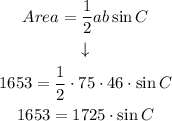
Finding C

We want to solve this equation for C:

`\begin{gathered} 1653=1725\cdot\sin C \\ \downarrow \\ (1653)/(1725)=\sin C \\ \downarrow \\ 0.96=\sin C \end{gathered}`

Then

`\arcsin (0.96)=C`

We have that arcsin(0.96) have different possible values:

73.7º

106.3º

Since this angle is obtuse (higher than 90º) then, the correct angle for C might be 106.3º

Answer: the measure of the included angle is 106.3º