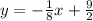Question

A line with a slope of -1/8 passes through the point ( 4,4).what is the equation in point -slope form

Answer 1

To determine the equation of the line, given that you know the slope and the coordinates of one point, you can use the point-slope form, which is:

`y-y_1=m(x-x_1)`

Where

m is the slope of the line

(x₁,y₁) are the coordinates of the point

Replace the values in the equation

m=-1/8

(x₁,y₁)= (4,4)

`y-4=-(1)/(8)(x-4)`

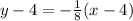
Next, write the equation in slope-intercept form:

-Distribute the multiplication in the parentheses term

`\begin{gathered} y-4=-(1)/(8)\cdot x-(-(1)/(8))\cdot4 \\ y-4=-(1)/(8)x-(-(1)/(2)) \\ y-4=-(1)/(8)x+(1)/(2) \end{gathered}`

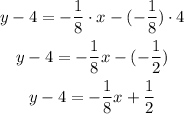
-Add 4 to both sides of the expression

`\begin{gathered} y-4+4=-(1)/(8)x+(1)/(2)+4 \\ y=-(1)/(8)x+(9)/(2) \end{gathered}`

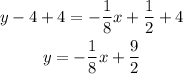
So, the equation of the line with slope -1/8 that passes through the point (4,4) is

`y=-(1)/(8)x+(9)/(2)`