Question

A tree was broken in a strong storm. The top part of the tree falls over and makes an angle of 56° with the ground. The horizontal distance from the base of the tree to the point where the top of the tree hits the ground is 110 feet. Find the height of the tree BEFORE it was broken showing.

Answer 1

Since the tree was broken and the top part forms an angle with the ground, therefore the height of the tree is x+y,

Given the horizontal distance and the angle formed with the ground,

`\begin{gathered} \theta=56^0 \\ \text{Adjcent = 110ft} \end{gathered}`

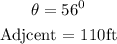
Using SOHCAHTOA, to find x (the vertical part of the broken tree),

`\begin{gathered} \tan \theta=(Opp)/(Adj) \\ \text{Opp = x} \\ \text{Adj = 110ft} \end{gathered}`

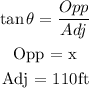
Substituting the values into the formula above,

`\begin{gathered} \tan 56^0=(x)/(110) \\ \text{Crossmultiply} \\ x=\tan 56*110=1.4826*110=163.1ft \end{gathered}`

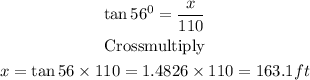
Using the Pythagorean theorem to find y,

`\begin{gathered} y^2=x^2+110^2 \\ y^2=163.1^2+110^2 \\ y^2=26601.61+12100 \\ y^2=38701.61 \\ y=\sqrt[]{38701.61} \\ y=196.7ft \end{gathered}`

The height of the tree before it got broken is,

`x+y=163.1+196.7=359.8ft`

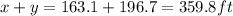
Hence, the height of the tree is 359.8 feet.