Question

If 2 tan^2 x -sec x = 1, which of the following are true? Select all that apply.

Answer 1

Given the equation:

`2tan^2x-secx=1`

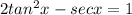
Let's find the true equations

First simplify using trigonometric identity

`2(sec^2x-1)-secx=1`

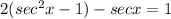
Apply distributive property:

`\begin{gathered} 2sec^2x-2-secx=1 \\ \\ Add\text{ 2 to both sides:} \\ 2sec^2x-2+2-secx=1+2 \\ \\ 2sec^2x-secx=3 \end{gathered}`

• Now, let's verify where: sec x = -1:

`\begin{gathered} 2(-1)^2-(-1)=3 \\ \\ 2+1=3 \\ \\ 3=3 \end{gathered}`

Hence, secx = 1 is true.

• For sec x = 3:

`\begin{gathered} 2(3)^2-3^2=3 \\ \\ 18-9=3 \\ \\ 9=3 \end{gathered}`

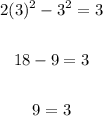
Hence, sec(x) = 3 is not true,

• For tanx = 3, we have:

Rewrite using trigonometric identity

`\begin{gathered} 2tan^2x-√(1+tan^2x)=1 \\ \\ 2(3)^2-√(1+(3)^2)=1 \\ \\ 18-√(10)=1 \end{gathered}`

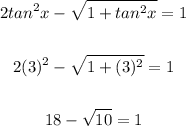
tan x = 3 is not true,

• For tanx = -1:

`\begin{gathered} 2tan^2x-√(1+tan^2x)=1 \\ \\ 2(-1)^2-√(1+(-1)^2)=1 \\ \\ -2-√(2)=1 \end{gathered}`

Hence tanx = -1 is not true.

• Now, for sec x = 3/2, we have:

`\begin{gathered} 2sec^2x-secx=3 \\ \\ 2((3)/(2))^2-((3)/(2))=3 \\ \\ 2((9)/(4))-(3)/(2)=3 \\ \\ (9)/(2)-(3)/(2)=3 \\ \\ 3=3 \end{gathered}`

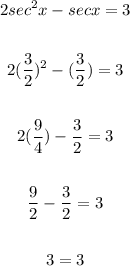
Hence, secx = 3/2 is true.

Therefore, the true equations are:

A. secx = -1

E. secx = 3/2

ANSWER:

A. sec x = -1

E. sec x = 3/2