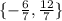Question

Solve the following Let f(x) = | 1-7x /3 | find all of x for which f (x) = 3

Answer 1

Given:

`f(x)=|(1-7x)/(3)|`

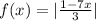
To find the values of x when f(x)=3, we apply below absolute rule:

If |u|=a, a>0 then, u=a or u= -a

Based on the above rule, our equations would be:

`1-(7x)/(3)=3`

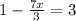
And,

`1-(7x)/(3)=-3`

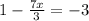
Next, we find x for 1-7x/3=3:

`\begin{gathered} 1-(7x)/(3)=3 \\ \text{Simplify and rearrange:} \\ (7x)/(3)=1-3 \\ (7x)/(3)=-2 \\ 7x=-2(3) \\ 7x=-6 \\ x=-(6)/(7) \end{gathered}`

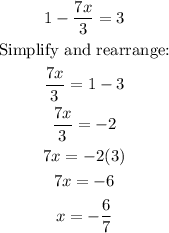
Then, we find x for 1-7x/3=-3:

`\begin{gathered} 1-(7x)/(3)=-3 \\ \text{Simplify and rearrange} \\ (7x)/(3)=1+3 \\ (7x)/(3)=4 \\ 7x=4(3) \\ 7x=12 \\ x=(12)/(7) \end{gathered}`

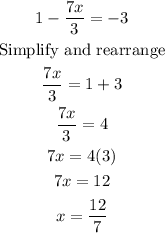
Therefore, the answer is A. The solution set is

`\lbrace-(6)/(7),(12)/(7)\rbrace`