Question

A student explored the relationship between normal force and acceleration while riding a special elevator at NASA. The student stood on a spring scale while the elevator accelerated upward and noted the scale reading. The student also explored how this experience affected the period of a pendulum, also along for the ride.Given:g earth = 10 m/s/sWeight of the student before getting into the elevator = 1000NScale reading while elevator was accelerating = 1100 NPeriod of pendulum while elevator was not moving = 3.0 sWhat was the period of the pendulum while the elevator was accelerating upward? 1.7 s2.5 s2.9 s3.0 s2.2 s1.9 s1.5 s

Answer 1

Here we can solve this question by the below equation,

`\begin{gathered} N=mg+ma\text{ }\rightarrow\text{ if elevator has upward accleration} \\ N=mg-ma\text{ }\rightarrow\text{ if elevator has downward accleration} \end{gathered}`

Here N = mass of the student When he is in the accelerated elevator.

mg is the mass of the student before entering the elevator

And (a) is the acceleration of the elevator

Now,

`\begin{gathered} Here, \\ N=1100N \\ mg=1000N \\ So\text{ }m=(1000)/(g)=(1000)/(10)=100kg \\ N=mg+ma \\ 1100=1000+100a \\ so,100a=1100-1000=100 \\ so,a=(100)/(100)=1\text{ m/s}^2 \end{gathered}`

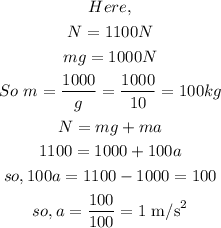
Now when elevator is accelerating upward the acceleration feel by the pendulum and the student will be = 10 + 1 = 11 m/s^2

And we know that time period of pendulum is,

`\begin{gathered} T=2\pi\sqrt[\placeholder{⬚}]{(l)/(g)} \\ When\text{ elevator was at rest then,} \\ l=((T)/(2\pi))^2g=((3)/(2*3.14))^210=0.228*10=2.28 \end{gathered}`

now when elevator is accelerated,

`T=2\pi\sqrt[\placeholder{⬚}]{(l)/(g)}=2*3.14*\sqrt[\placeholder{⬚}]{(2.28)/(11)}=\text{ 2.85}`

so o