Question

A certain type of apple, when mature, has mean weight of 6.73 ounces with a population standard deviation of 1.84. if sample of 40 apples was taken, what is the probability it would have a sample mean weight of greater than 7 ounces?

Answer 1

Given information:

Population Mean = 6.73 ounces

Population SD = 1.84

sample size = 40

sample mean > 7 ounces

To solve the probability of a sample mean greater than 7 ounces, we need to transform the sample mean to a standard normal variable using the formula below

`Z=\frac{\text{sample mean-population mean}}{(\frac{population\text{ standard deviation}}{sqrt\text{ of sample size}})}`

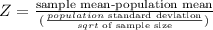
With the above formula, let's now substitute the given information above to convert the sample mean to Z.

`\begin{gathered} Z=\frac{7-6.73}{(\frac{1.84}{\sqrt[]{40}})} \\ Z=(0.27)/(0.2909295447) \\ Z\approx0.93 \end{gathered}`

Looking at the z-table, the area greater than 0.93 is 0.1762. Therefore, the probability greater of having a sample mean greater than 7 ounces is 17.62%. Have a look at the illustration below.

The yellow side is the area less than 7 ounces.

The blue side is the area greater than 7 ounces.