Given:
The center of circle A is (6,5).
The radius of the circle is 2 units.
The point on the tangent is C(1,3).
Required:
We need to find the equation of the tangent.
Step-by-step explanation:
The tangent is a straight line which is of the form

Where m is the slope of the tangent.
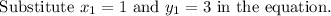

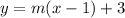
Consider the circle equation.

Substitute h =6, k=5, and r =2 in the formula.
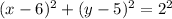

Substitute x=1 in the equation, and we get
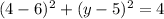
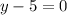
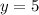
We get the point that lies in the circle is (4,5).
Use the points (4,5) and (6,5) to find the slope of the radius.
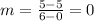
We know that the radius and tangent are perpendicular to each other.
The slope of the perpendicular lines is negative reciprocal.
The slope of teh tangent line is again zero.
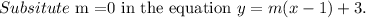
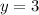
Final answer:
The equation of the tangent line from point C(1,3) is
