Given the functions:
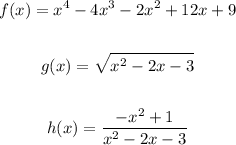
Let's answer the following questions.
• (a). Let's compare the domain and range of f(x) and g(x) using statements.
Domain and range of f(x):
Since f(x) is a polynomial function, the domain will be all real numbers:
Domain: (-∞, ∞)
The range will be:
Range: [0, ∞)
• Domain and range of g(x):
The domain of g(x) is:
Domain: (-∞, -1] ∪ [3, ∞)
The range of g(x) is:
[0, ∞)
Therefore, using complete statements, we have:
The domain and range of f(x) are D(-∞, ∞) and R [0, ∞), while the domain and range of g(x) are D(-∞, -1] ∪ [3, ∞) and R[0, ∞)
• (b). The breaks of the function h(x) is defined by the denominator of the rational function h(x)
Using the function, h(x), the zeros of the denominator are:
x = -3, 1
The zeros of f(x), are:
x = -3, 1
Therefore, the breaks in the domain of h(x) are at x = -3 and x = 1 which is equal and located at the same point as the zeros of the domain of f(x).
ANSWER:
• (a). The domain and range of f(x) are D(-∞, ∞) and R [0, ∞), while the domain and range of g(x) are D(-∞, -1] ∪ [3, ∞) and R[0,, ,∞).
• (b). The breaks in the domain of h(x) are at x = -3 and x = 1 which is equal and located at the same points as the zeros of the domain of f(x).