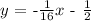Question

write the equation of a line perpendicular to the line that passes through the given point.
`(1)/(2)y = 8x + 3 = 0`(-8,0)

Answer 1

Given the equation:

`(1)/(2)y=8x+3`

Rewrite the equation in slope intercept form:

y = mx + b

Multiply both through by 2

`\begin{gathered} (1)/(2)y\ast2=\text{ }8x\ast2\text{ + 3}\ast2 \\ \\ y\text{ = 16x + 6} \end{gathered}`

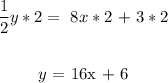
The slope of this line is 16.

therefore, the slope of the line perperndicular to it will be it's inverse:

`-(1)/(16)`

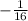
The perpendicular line has the points:

(x, y) ===> (-8, 0)

We have:

y = mx + b

`0\text{ =-}(1)/(16)(-8)+b`

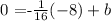
Solve for b which is the y-intercept:

`\begin{gathered} 0\text{ = }(1)/(2)+b \\ \\ b\text{ = -}(1)/(2) \end{gathered}`

Since the y intercept is -½

slope = -1/16

The equation of the line in point slope form:

(y - y1) = m(x - x1)

`(y\text{ - 0) = -}(1)/(16)(x\text{ + 8)}`

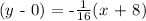
Therefore, the equation of the perpendicular line in slope intercept is:

`y\text{ = -}(1)/(16)x\text{ - }(1)/(2)`