There are two possible solutions for the triangle. For both, we can use the Law of sines.
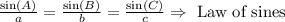
Then, we have:
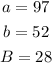
First possible solution
We find the angle A:

We find the angle C using the angle sum theorem, which says that the sum of measures of interior angles of a triangle is 180°.
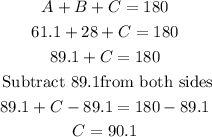
We find the side c:

Second possible solution
We find the angle A:
![\begin{gathered} (\sin(A))/(a)=(\sin(B))/(b) \\ (\sin(A))/(97)=(\sin(28))/(52) \\ \text{ Multiply by 97 from both sides of the equation} \\ (\sin(A))/(97)\cdot97=(\sin(28))/(52)\cdot97 \\ \sin (A)=(97\sin(28))/(52) \\ \sin (A)=0.8757 \\ \text{ We apply the inverse function }\sin ^(-1)(x)\text{ from both sides of the equation and we subtract this value from 180\degree} \\ 180\text{\degree}-\sin ^(-1)(\sin (A))=180\text{\degree}-\sin ^(-1)(0.8757) \\ A\approx180\text{\degree}-61.1\text{\degree} \\ A\approx118.9\text{\degree} \end{gathered}]()
We find the angle C using the angle sum theorem:
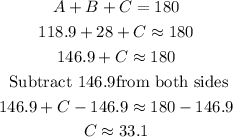
We find the side c:
