Solution
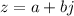
The rectangular form of a complex form is given in terms of 2 real numbers a and b in the form: z=a+jb
The polar form of the same number is given in terms of a magnitude r (or length) and argument q (or angle) in the form: z=r|_q
You can "see" a complex number on a drawing in this way:

In this case the numbers a and b become the coordinates of a point representing the complex number in the special plane (Argand-Gauss) where on the x axis you plot the real part (the number a) and on the y axis the imaginary (the b number, associated with j).
Therefore the correct answer is -5 + 2i
Hence the answer is Option D