To solve for the height of the container, we will have to multiply the diameter of the balls by 3.
Height of the container= 3×diameter of the spherical ball
where the diameter of the ball= 2.7 in
Height of the container= 3×2.7in
= 8.1 in
Height of the container= 8.1 in
To find the unused volume in the can, we have to find the Volume of the three spherical balls and subtract it from the volume of the cylindrical can.
Unused volume in the can = Volume of the can - 3(Volume of the spherical ball)
Formula for the volume of the can

Formula for the volume of the spherical balls

The volume above is the volume of one spherical ball, so the Volume of the three numbers of the spherical ball will be equal to three times the volume of one ball.
Volume of three spherical balls = 3× 10.3in= 30.9 in³
Therefore,
The volume of the unused in the can= 46.35 in³- 30.9in³
Unused volume in the can= 15.45 in³
For number C, the mistake the boy did was that the boy solved for the surface area of the ball instead of the volume of one ball. It would be shown below mathematically.
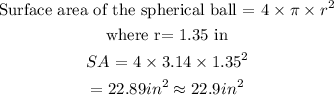
For D, the total volume of the can=46.35 in³.
Unused volume= 15.45in³≈ 15.5in³ (nearest tenth)
For F, we were told to solve for the curve surface area of the cylinder

Hence the dimensions of the label= 8.5×8.1 in²