Question

A can of soda is placed inside a cooler. As the soda cools, its temperature Tx in degrees Celsius is given by the following function, where x is the number of minutes since the can was placed in the cooler.=Tx+−826e−0.05xFind the temperature of the soda after 8 minutes and after 15 minutes. Round your answers to the nearest degree as necessary.

Answer 1

Given:

`T(x)=-8+26e^(-0.05x)`

where:

x= 8, 15

To determine the temperature after 8 minutes, we plug in x=8 into the given function as shown below:

`\begin{gathered} T(x)=-8+26e^(-0.05x) \\ T(8)=-8+26e^(-0.05(8)) \\ Calculate \\ T(8)=9.4 \\ T(8)=9\degree C \end{gathered}`

To determine the temperature after 15 minutes, we plug in x=15 into the given function:

`\begin{gathered} T(x)=-8+26e^(-0.05x) \\ T(15)=-8+26e^(-0.05(15)) \\ Calculate \\ T(15)=4.3 \\ T(15)=4\degree C \end{gathered}`

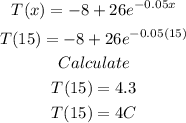
Therefore, the answers are:

Temperature after 8 minutes : 9 °C

Temperature after 15 minutes : 4 °C