Question

Two dice are rolled. Determine the probability of the following.Rolling an even number or a number greater than 7

Answer 1

We are given that two dices are rolled. Since each dice has numbers from 1 to 6, the total possible outcomes are:

`\begin{gathered} (1,1)(1,2)(1,3)(1,4)(1,5)(1,6) \\ (2,1)(2,2)(2,3)(2,4)(2,5)(2,6) \\ (3,1)(3,2)(3,3)(3,4)(3,5)(3,6) \\ (4,1)(4,2)(4,3)(4,4)(4,5)(4,6) \\ (5,1)(5,2)(5,3)(5,4)(5,5)(5,6) \\ (6,1)(6,2)(6,3)(6,4)(6,5)(6,6) \end{gathered}`

We are asked to determine the probability of getting an even number or a number greater than 7.

To do that we will use the following relationship:

`P(A\text{ or B\rparen=}P(A)+P(B)`

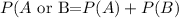
Where:

`\begin{gathered} A=\text{ even number} \\ B=\text{ number greater than 7} \end{gathered}`

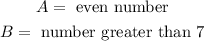
To determine the probability of getting an even number we need to determine the number of outcomes where there is an even number. Those outcomes are:

`\begin{gathered} (1,2)(1,4)(1,6) \\ (2,1)(2,2)(2,3)(2,4)(2,5)(2,6) \\ (3,2)(3,4)(3,6) \\ (4,1)(4,2)(4,3)(4,4)(4,5)(4,6) \\ (5,2)(5,4)(5,6) \\ (6,1)(6,2)(6,3)(6,4)(6,5)(6,6) \end{gathered}`

There are a total of 27 outcomes where there is an even number out of a total of 36 possible outcomes, therefore, the probability of getting an even number is:

`P(A)=(27)/(36)`

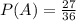
To determine the number of outcomes where there is a number greater than 7 we notice that since each dice is numbered from 1 to 6 this means that there is no number greater than 7 therefore, the probability is zero:

`P(B)=(0)/(36)=0`

Substituting in the formula for both probabilities we get:

`P(AorB)=(27)/(36)+0=(27)/(36)`

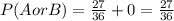
Therefore, the probability of getting an even number or a number greater than 7 is 27/36.