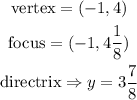Question

Drag the labels to the correct locations on the table. Not all tiles will be used. Match each attribute of a parabola to the correct quadratic function. vertex: (-1,4) (-1,34 focus: focus: (1,3) directrix: Y=35 directrix: y=4 vertex: (-1,-4) vertex: (1,4) focus: (-1,4) directrix: y=3 : : f(x) = -(x - 1)2 + 4 f(x) = 2(x + 1)2 + 4

Answer 1

First equation

`f(x)=-(x-1)^2+4`

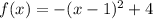
The general form of a parabola is given as

`y=a(x-h)+k`

Comparing the general form with the first equation

`a=-1,h=1,k=4`

The vertex of a parabola is given as

`Vertex=(h,k)`

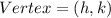
Therefore, the vertex of the first parabola is (1, 4)

The focus of a parabola is given as

`Focus=(h,k+(1)/(4a))`

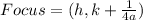
Substitute the values of h, k and a into the formula for focus

This gives

`\begin{gathered} \text{Focus}=(1,4+(1)/(4(-1))) \\ \text{Focus}=(1,4+(1)/(-4)) \\ \text{Focus}=(1,(15)/(4)) \\ \text{Focus}=(1,3(3)/(4)) \end{gathered}`

Therefore, the focus of the first equation is

`\text{Focus=}(1,3(3)/(4))`

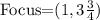
The directrix of the parabola will have the equation

`y=k-(1)/(4a)`

Substituting values gives

`\begin{gathered} y=4-(1)/(4(-1)) \\ y=4-(1)/(-4) \\ y=4+(1)/(4) \\ y=(17)/(4) \\ y=4(1)/(4) \end{gathered}`

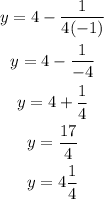
The directrix of the first equation has the eqaution

`y=4(1)/(4)`

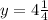
Therefore, all the attribute of the first equation are

`\begin{gathered} \text{vertex}=(1,4) \\ \text{focus}=(1,3(3)/(4)) \\ \text{directrix}\Rightarrow y=4(1)/(4) \end{gathered}`

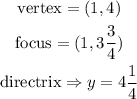
For the second equation

`y=2(x+1)^2+4`

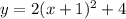
Comparing with the general form of a parabola

It follows

`a=2,h=-1,k=4`

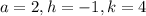
Following the calculations as above

Then

All the attributes of the second equations are

`\begin{gathered} \text{vertex}=(-1,4) \\ \text{focus}=(-1,4(1)/(8)) \\ \text{directrix}\Rightarrow y=3(7)/(8) \end{gathered}`