Given: The systems of equation below
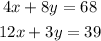
To Determine: The solution of the system of equations using elimination method
Eliminate x
To eliminate x, multiply the first equation by 3 and the second equation by 1
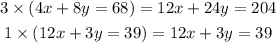
Combine two equations by subtracting the second equation from the first
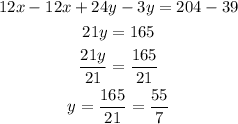
Substitute y in the first equation to get x
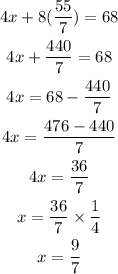
Hence, the solution is
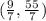
(9/7 , 55/7)