Question

An 76,900 liter swimming pool has a chlorine concentration of 2.6 ppm (parts per million). How many liters must be replaced with 20 ppm chlorine solution to increase the chlorine concentration to 4 ppm? Round your final answer to 1 decimal place if necessary.

Answer 1

Given:

A 76,900-liter swimming pool has a chlorine concentration of 2.6 ppm.

To find:

How many liters must be replaced with 20 ppm chlorine solution to increase the chlorine concentration to 4 ppm?

Solution:

The concentration in terms of ppm is given by:

`ppm=\frac{mass\text{ of solute}}{mass\text{ of solution}}*10^6`

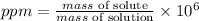
So, the mass of solute becomes:

`mass\text{ of solute}=\frac{mass\text{ of solution}* ppm}{10^6}`

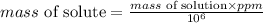
Let x mL of the pool solution is replaced by 20 ppm chlorine solution to make final chlorine concentration equal to 4 ppm. So,

`\begin{gathered} (x*20)/(10^6)+((76900000-x)2.6)/(10^6)=(76900000(4))/(10^6) \\ 20x+199940000-2.6x=307600000 \\ 17.4x=107660000 \\ x=(107660000)/(17.6) \\ x=6117045.455\text{ mL} \\ x=6117.1L \end{gathered}`

Thus, the answer is 6117.1 L.