Answer:
Ques 1:
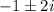
Ques 2:
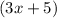
Explanation:
The quadratic formula states that the roots of the equation,
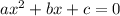 are given by,
are given by,
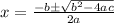 .
.
Ques 1: The quadratic equation is given by,
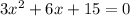 .
.
On comparing, a= 3, b= 6 and c= 15.
So, the roots of the equation are given by,
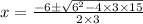
i.e.
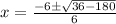
i.e.
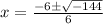
i.e.
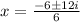
i.e.
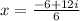 and i.e.
and i.e.
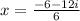
i.e.
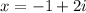 and i.e.
and i.e.
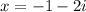
Thus, the solutions of the equation are
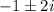 .
.
Ques 2: The quadratic equation is
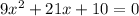 .
.
On comparing, a= 9, b= 21 and c= 10.
So, the roots of the equation are given by,
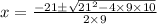
i.e.
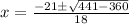
i.e.

i.e.
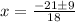
i.e.
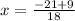 and i.e.
and i.e.

i.e.
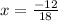 and i.e.
and i.e.
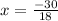
i.e.
 and i.e.
and i.e.
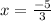
That is, the factors are
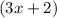 and
and
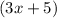
So, according to the options,
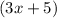 is the correct option.
is the correct option.