First, we express the following by supplementary angles.
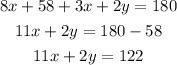
Then, we use the interior angles theorem which states that the sum of all three interior angles of a triangle is 180°.
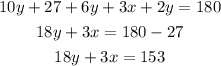
Now, we form a system of linear equations with the equations we found.
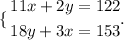
Let's multiply the first equation by -9 to sum them and eliminate y.

Then, we find y.
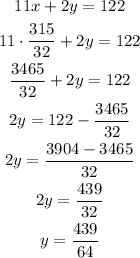
Hence, x is equal to 315/32 and y is equal to 439/64.