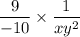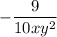Question

This is on 9.1 puzzle time what do you say when you get off a boat?

Answer 1

The solution to the surd is
`-(9)/(10xy^2 ) }`

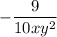
Simplification of surds.

In mathematics, Surd is a term that refers to square roots or other roots that cannot be stated exactly as a finite fraction or decimal. Surds are simplified when they are expressed in a more simpler form while preserving their actual value.

In the given question, we have:

`\sqrt[3]{(729)/(-1000x^3y^6)}`

First simplify the fraction;

`\sqrt[3]{(729)/(-1000) * (1)/(x^3y^6)}`

Taking the cube root.

`(9)/(-10) * \frac{1}{\sqrt[3]{x^3y^6}}`

`(9)/(-10) * (1)/(xy^2)}`

`-(9)/(10xy^2 ) }`

Answer 2

In order to find the answer, we must first simplify the expression.
∛(729) = 9
∛(-1000) = -10
∛(x)³ = x
∛(y)⁶ = y²


The expression subsequently becomes:
9 / -10xy²

From the key that is provided next to the puzzle, we see that this expression represents the letter "M". The phrase is figured out using the remaining letters.