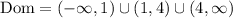Question

Suppose that the functions f and g are defined as follows F(x)=x-1 g(x)=x-1/x-4Find f/g then give its domain using an interval or union of intervals Simplify your answer as much as possible (f/g)(x)=Domain of f/g:

Answer 1

We have:

`\begin{gathered} f(x)=x-1 \\ g(x)=(x-1)/(x-4) \end{gathered}`

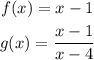
And we must find the quotient f/g. So let's take f and divide it by g:

`\begin{gathered} (f)/(g)(x)=(f(x))/(g(x))=(x-1)/((x-1)/(x-4))=(x-1)\cdot(x-4)/(x-1)=x-4 \\ (f)/(g)(x)=x-4 \end{gathered}`

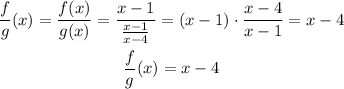
So the result is x-4. In order to calculate its domain we must take into acount that it was made from dividing f by g so this isn't a simple linear function with a domain from negative infinite to positive infinite. Any number that isn't part of the domain of g or that makes g=0 is a number that doesn't belong to the domain of f/g either. Values that aren't part of the domain of g are those who make its divider equal to 0 so we have:

`\begin{gathered} x-4=0 \\ x=4 \end{gathered}`

The values that make g=0 are those which make its dividend equal to 0:

`\begin{gathered} x-1=0 \\ x=1 \end{gathered}`

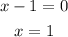
All these calculation mean that the values 1 and 4 are not part of f/g domain. Then the domain can be written as:

`\text{Dom}=(-\infty,1)\cup(1,4)\cup(4,\infty)`