Question

find the value of the ordinary annuity at the end of the indicated time period. The payment R, frequency of deposits, m, (same as the frequency of compounding), annual interest rate r, and time t, are given below:Amount, $500; monthly; 3% ; 3 years (36 months)

Answer 1

Remember that

The formula for the future value of an ordinary annuity is equal to:

`FV=P\lbrack((1+ (r)/(n) )^(nt) -1)/( (r)/(n) )\rbrack`

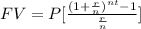
where

FV is the future value

P is the periodic payment

r is the interest rate in decimal form

n is the number of times the interest is compounded per year

t is the number of years

In this problem we have

P=$500

r=3%=0.03

t=3 years

n=12

substitute in the formula

`FV=500\lbrack((1+(0.03)/(12))^(12\cdot3)-1)/((0.03)/(12))\rbrack`

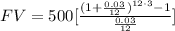
FV=$18,810.28