Question

The length of a rectangle is three inches more than the width. the area of the rectangle is 180 inches. find the width of the rectangle

Answer 1

We have a rectangle with length L that is 3 inches more than the width W. Then we can write this as:

`L=W+3`

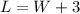
The area of the rectangle is 180 square inches.

We have to find the width W.

As the area is equal to the product of the length and the width, we can write this equation and solve for W as:

`\begin{gathered} A=180 \\ L\cdot W=180 \\ (W+3)\cdot W=180 \\ W^2+3W=180 \\ W^2+3W-180=0 \end{gathered}`

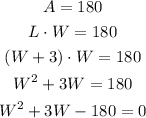
We have a quadratic equation. The roots of this equation will be the mathematical solutions.

We can find the roots using the quadratic formula:

`\begin{gathered} W=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ W=\frac{-3\pm\sqrt[]{3^2-4\cdot1\cdot(-180)}}{2\cdot1} \\ W=\frac{-3\pm\sqrt[]{9+720}}{2} \\ W=\frac{-3\pm\sqrt[]{729}}{2} \\ W=(-3\pm27)/(2) \\ W_1=(-3-27)/(2)=-(30)/(2)=-15 \\ W_2=(-3+27)/(2)=(24)/(2)=12 \end{gathered}`

The solutions are W = -15 and W = 12.

The first one is not valid, as W has to be greater than 0.

Then, the solution to our problem is W = 12 in.

Answer: the width is W = 12 inches.