Question

The population P (in thousands) of a certain city from 2000 through 2014 can be modeled by P = 120.7e^(kt)where t represents the year, with t = 0 corresponding to 2000. In 2009, the population of the city was about 167,025.(a) Find the value of k. (Round your answer to four decimal places.)k = Incorrect: Your answer is incorrect.Is the population increasing or decreasing? Explain.Because k is negative, the population is increasing.Because k is positive, the population is increasing. Because k is negative, the population is decreasing.Because k is positive, the population is decreasing.Correct: Your answer is correct.(b) Use the model to predict the populations of the city (in thousands) in 2020 and 2025. (Round your answers to three decimal places.)2020 P = thousand people2025 P = thousand peopleAre the results reasonable? Explain.The populations are not reasonable. The population cannot continue to increase at the same rate it did from the year 2020 to 2025.The populations are reasonable if it continues to increase at the same rate from the year 2020 to 2025. Correct: Your answer is correct.(c) According to the model, during what year will the population reach 220,000?

Answer 1

ANSWER and EXPLANATION

(a) To find the value of k, we substitute the given values of t and P for the year 2009.

In 2009, we have that:

`\begin{gathered} t=9\text{ years} \\ P=167,025 \end{gathered}`

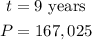
Substituting that, we have:

`\begin{gathered} 167,025=120.7\cdot e^(k\cdot9)\cdot1000 \\ \Rightarrow=(167,025)/(120,700)=e^(9k) \\ 1.3838=e^(9k) \end{gathered}`

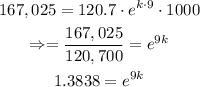
Transform the equation from an exponential equation to a logarithmic equation:

`\begin{gathered} \ln 1.3838=\ln (e^(9k)) \\ \Rightarrow9k=0.3248 \\ \Rightarrow k=(0.3248)/(9) \\ k=0.0361 \end{gathered}`

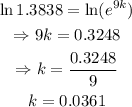
That is the value of k.

Since k is positive, the population is increasing.

(b) In 2020, t will be equal to 20, since 2020 is 20 years after 2000.

Therefore, we have that the population will be:

`\begin{gathered} P=120.7e^((0.0361\cdot20)) \\ P=248.467\text{ thousand people} \end{gathered}`

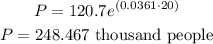
That will be the population in 2020.

In 2025, t will be equal to 25.

Therefore, we have that the population will be:

`\begin{gathered} P=120.7\cdot e^((0.0361\cdot25)) \\ P=297.617\text{ thousand people} \end{gathered}`

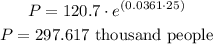
That will be the population in 2025.

The populations are reasonable since it continues to increase from the years 2020 to 2025.

(c) To find the year that the population will reach 220,000, we have to find the value of t when P is 220 (since P is given in thousands).

Therefore, we have:

`\begin{gathered} 220=120.7e^((0.0361\cdot t)) \\ (220)/(120.7)=e^((0.0361t)) \\ 1.8227=e^(0.0361t) \end{gathered}`

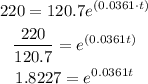
Transform the equation into a logarithmic equation:

`\begin{gathered} \ln 1.8227=\ln (e^(0.0361t)) \\ 0.6003=0.0361t \\ \Rightarrow t=(0.6003)/(0.0361) \\ t=16.6\text{ years} \end{gathered}`

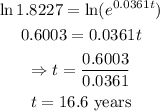
In other words, the population will reach 220,000 in the 16th year after 2000 i.e. 2016.