Question

Two friends visited Washington D.C. for the weekend. Person 1 rode the subway three times at the peak fare price and five times at the off-peak fare price for a total cost of $19.50. Person 2 rode two times at the peak fare price and four times at the off-peak fare price for a total cost of $14.50. How much was the peak fare price?

Answer 1

We are given the following information.

Person 1 rode the subway three times at the peak fare price and five times at the off-peak fare price for a total cost of $19.50.

Person 2 rode two times at the peak fare price and four times at the off-peak fare price for a total cost of $14.50.

We are asked to find the peak fare price.

Let x represent the peak fare price.

Let y represent the off-peak fare price.

Then we can set up the following two equations for persona 1 and person 2.

`\begin{gathered} 3x+5y=19.50\;\;eq.1 \\ 2x+4y=14.50\;\;eq.2 \end{gathered}`

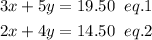
Separate out the y variable in eq.1

`\begin{gathered} 3x+5y=19.50 \\ 5y=19.50-3x \\ y=(19.50-3x)/(5) \end{gathered}`

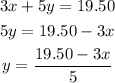
Now, substitute it into eq.2

`\begin{gathered} 2x+4y=14.50 \\ 2x+4((19.50-3x)/(5))=14.50 \\ 2x+(78-12x)/(5)=14.50 \\ (5\cdot2x+78-12x)/(5)=14.50 \\ (10x+78-12x)/(5)=14.50 \\ 10x-12x+78=14.50\cdot5 \\ -2x+78=72.5 \\ -2x=72.5-78 \\ -2x=-5.5 \\ 2x=5.5 \\ x=(5.5)/(2) \\ x=\$2.75 \end{gathered}`

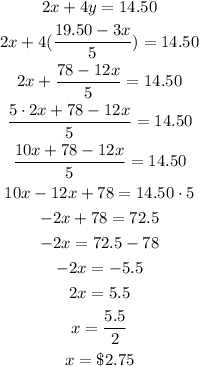
Therefore, the peak fare price is $2.75