Question

Which trig expression is equal to sin (72° - a)?

A) cos 18°
B) sin 18°
C) cos (90° - (72° - a))
D) sin (90° - (72° - a ))

Answer 1

C c c c c c c c c c c

Answer 2

Answer: The correct option is (C)
`\cos(90^\circ-(72^\circ-a)).`

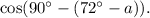
Step-by-step explanation: We are given to select the correct trigonometric expression that is equivalent to the following expression:

`E=\sin(72^\circ-a).`

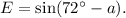
We know that the sine and cosine of any acute angle are complementary to each other.

That is, if 'x' is any acute angle, then

`\sin(90^\circ-x)=\cos x,\\\\\textup{and}\\\\\cos(90^\circ-x)=\sin x.`

Since (72° - a) is an acute angle, so we must have

`E=\sin(72^\circ-a)=\cos(90^\circ-(72^\circ-a)).`

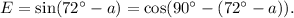
Thus, the correct equivalent expression is
`\cos(90^\circ-(72^\circ-a)).`

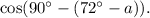
Option (C) is correct.