Question

The fuel efficiency, in miles per gallon, of 10 small utility trucks was measured. The results are recorded in the table below.Fuel Efficiency (mpg)232524271423243323222523Find the mean and sample standard deviation of these data. Round to the nearest hundredth.mean ________ sample standard deviation _______

Answer 1

The mean is the average of the given numbers, that is,

`\begin{gathered} \bar{x}=(23+25+24+27+14+23+24+33+23+22+25+23)/(12) \\ \bar{x}=23.8333 \end{gathered}`

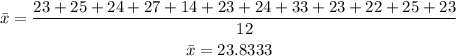
In order to find the sample standard deviation, we need to find the variance S^2. It is given by

`S^2=\frac{\sum ^(12)_(n\mathop=1)(x_n-\bar{x})}{n-1}`

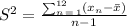
since there are 12 values (n=12) ,we have

`S^2=((23-23.833)^2+(25-23.833)^2+\cdots+(23-23.833)^2)/(11)`

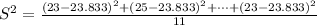
which gives

`S^2=18.151515`

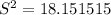
Since the sample standard deviation is the square root of the variance, we have

`\begin{gathered} S=\sqrt[]{18.1515} \\ S=4.26 \end{gathered}`

Therefore, by rounding to the nearest hundreadth, the answers are: