Question

A 54-inch pendulum swings at an angle of 20°. Find the length of the arc to the nearest hundredth of aninch through which the tip of the pendulum swings.anglerin.

Answer 1

18.85 inches

Explanation:

In any circle, the length of an arc on the circle is calculated using the formula below:

`\text{Length}=(\theta\pi r)/(180)`

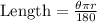
Given:

• The length of the pendulum = 54 inches

,

• Central Angle, θ = 20°

Substitute into the formula:

`L=(20(\pi)(54))/(180)\approx18.85\text{ inches}`

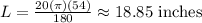
The length of the arc through which the tip of the pendulum swings is 18.85 inches (to the nearest hundredth).