Question

please help me ASAPif asked is this a text or a quiz this is a practiceif asked if a agree to the terms and guidelines I agree

Answer 1

`Tn\text{ = -}(4)/(3)(-3)^(n-1)`

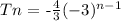
Step-by-step explanation:

The nth term of a geometric sequence is expressed as;

`\text{T}_{n\text{ }}=ar^(n-1)`

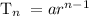
If the second term is 4;

`\begin{gathered} T_2=\text{ ar} \\ T_{2\text{ }}=\text{ ar= 4} \end{gathered}`

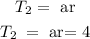
If the third term is -12, hence;

`\text{T}_{3\text{ }}=ar^2\text{= -12}`

Solve equation 1 and 2 simultaneously for a and r

Divide both expressions

`\begin{gathered} (ar)/(ar^2)=\text{ }(4)/(-12) \\ (1)/(r)=(4)/(-12) \\ r\text{ = -12/4} \\ r\text{ = -3} \end{gathered}`

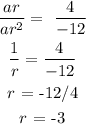
Get the first term;

Substitute r = -3 into 1;

Frm 1;

`\begin{gathered} ar\text{ = 4} \\ -3a\text{ = 4} \\ a\text{ = }(-4)/(3) \end{gathered}`

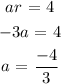
Get the explicit expression;

`\begin{gathered} Tn=ar^(n-1) \\ Tn\text{ =-}(4)/(3)(-3)^{n-1^{}^{}} \end{gathered}`

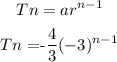
This gives the required answer