Question

The heights of a certain group of adult males was found to be normally distributed. The mean height is 170 cm with a standard deviation of 6 cm. In a group of 1200 of these males, about how many would be more than 164 cm tall?

Answer 1

Answer: C

Explanation:

Dude trust me

Answer 2

To find the number of males from the new sample, we first need to compute for the z-score as shown below.


`Z = (\chi - \mu)/(\sigma)`

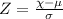
where Χ is the mean height we want to check, μ is the expected mean of the height, δ is the standard deviation, and n is the number of samples. Since, we have all of these information at hand, we can now compute for the z-score of the sample.


`Z = (164 - 170)/(6)`

`Z = -1`

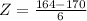
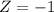
Now, using the z-table, we can find its p-value which we'll be using to find the number of males. Since z-score is -1, we have P(z > 0.158655) = 1 - 0.158655 = 0.841345.

This signifies the percent of the total population that has a height of more than 164. So, out of 1200, we have 0.841345(1200) = 1009.614 ≈ 1010.

Therefore, we've seen that there are approximately 1010 male from the sample that will have a height of more than 164.

Answer: 1010