Question

TRIGONOMETRY Find the area of the entire region round to two decimal places

Answer 1

65.79 sq units

Step-by-step explanation:

We are given this:

Sides of triangle = 8 units

Interior angle between the sides = 72.6 degrees

The sum of the interior angles in a triangle is 180 degrees:

`\begin{gathered} 72.6+x+x=180 \\ 72.6+2x=180 \\ \text{Subtract ''72.6'' from both sides, we have:} \\ 2x=180-72.6 \\ 2x=107.4 \\ x=(107.4)/(2)=53.7 \\ x=53.7^(\circ) \end{gathered}`

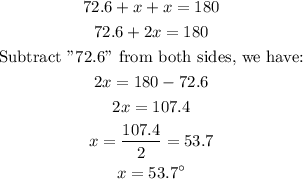
We will obtain the value for the base of the triangle using the Sine rule, we have:

`\begin{gathered} (\sin A)/(a)=(\sin B)/(b)=(\sin C)/(c) \\ (\sin72.6^(\circ))/(a)=(\sin53.7^(\circ))/(8)=(\sin53.7^(\circ))/(8) \\ (\sin72.6^(\circ))/(a)=(\sin53.7^(\circ))/(8) \\ \text{Cross multiply, we have:} \\ a\cdot\sin 53.7^(\circ)=8*\sin 53.7^(\circ) \\ a=(8*\sin72.6^(\circ))/(\sin53.7^(\circ)) \\ a=(8*0.9542)/(0.8059) \\ a=9.4721\approx9.47 \\ a=9.47units \end{gathered}`

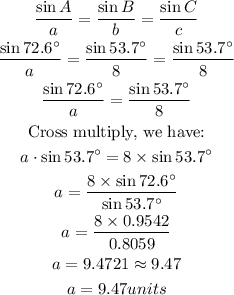
The base of the triangle is 9.47 units

We will thus find the area of the figure as shown below:

`\begin{gathered} Area=Area_(triangle)+Area_(semi-circle) \\ \text{ We will use Heron's formula to calculate the area of the triangle:} \\ Area_(triangle)=\sqrt[]{s(s-a)(s-b)(s-c)} \\ s=(a+b+c)/(2)=(8+8+9.47)/(2)=12.7360\approx12.74 \\ Area_(triangle)=\sqrt[]{12.74(12.74-9.47)(12.74-8)\mleft(12.74-8\mright)} \\ Area_(triangle)=\sqrt[]{12.74(3.27)(4.74)(4.74)} \\ Area_(triangle)=\sqrt[]{935.99572248} \\ Area_(triangle)=30.5940\approx30.59 \\ \\ Area_(semi-circle)=(1)/(2)\pi r^2 \\ Area_(semi-circle)=(1)/(2)*3.14*4.735^2 \\ Area_(semi-circle)=35.19975\approx35.20 \\ Area_(semi-circle)=35.20 \\ \\ Area=30.59+35.20=65.79 \\ \therefore Area=65.79units^2 \end{gathered}`

Therefore, the area of the shape is 65.79 sq units