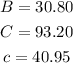Question

Use the Law of Sines to solve (if possible) the triangle. If two solutions exist, find both. Round your answers to two decimal places. (If not possible, enter IMPOSSIBLE.)A = 56°, a = 34, b = 21

Answer 1

Remember that the vertices and the sides of the triangles are usually labelled according to their locations as follows:

Side a is opposite to the angle A and so on.

According to the Law of Sines:

`(a)/(\sin(A))=(b)/(\sin(B))=(c)/(\sin(C))`

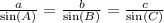
Since A, a and b are known, then, we can use the Law of Sines to determie the value of B. First, solve for B using the inverse sine function:

`\begin{gathered} (a)/(\sin(A))=(b)/(\sin(B)) \\ \\ \Rightarrow\sin(B)=(b)/(a)\sin(A) \\ \\ \Rightarrow B=\sin^(-1)\left((b)/(a)\sin(A)\right) \end{gathered}`

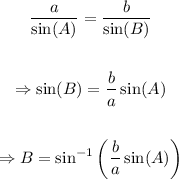
Replace b=21, a=34 and A=56º to find the value of B:

`B=\sin^(-1)\left((21)/(34)\sin(56º)\right)=30.8º`

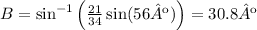
Now, we know two internal angles of the triangle: A and B. Since the sum of the internal angles of any triangle must be equal to 180º, we can use that to find the valu of C:

`\begin{gathered} A+B+C=180º \\ \Rightarrow C=180º-A-B \\ \Rightarrow C=180º-56º-30.8º \\ \therefore C=93.2º \end{gathered}`

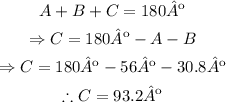
Finally, sine we know A, a and C, we can use the law of sines again to find c:

`\begin{gathered} (c)/(\sin(C))=(a)/(\sin(A)) \\ \\ \Rightarrow c=(\sin(C))/(\sin(A))* a=(\sin(93.2º))/(\sin(56º))*34=40.947...\approx40.95 \end{gathered}`

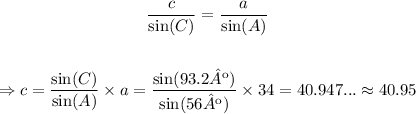
Therefore, to two decimal places, the answers are:

`\begin{gathered} B=30.80 \\ C=93.20 \\ c=40.95 \end{gathered}`