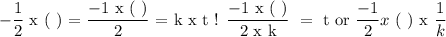Question

The law of reaction rate: 2 N2O => 2N2 (g) + O2 (g) is of order two with respect to N2O. The reaction carried out at 900K with an initial concentration of N2O equal to 2 × 10 ^ -2 mol / L. It took 4500 seconds for N2O to drop to half of its initial concentration. Calculate: The time required for N2O to decompose to 90% of its initial concentration.

Answer 1

2 N2O => 2N2 (g) + O2 (g)

We have an order to respect N2O, so:

`r\text{ = -}(1)/(2)(d\lbrack N2O\rbrack)/(dt)=k\text{ x }\lbrack N2O\rbrack^2`

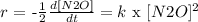
It says the reaction was carried out at 900K, so k doesn't change.

k depends on the temperature. That is important when we want to integrate.

Units:

`\lbrack r\text{ }\rbrack=\frac{mol}{L\text{ s}}\text{ ; }\lbrack N2O\rbrack=\text{ }(mol)/(L)\text{ ; }\lbrack k\rbrack=\text{ }\frac{L}{\text{mol s}}`

Let's separate variables and then integrate.

`-(1)/(2)\int ^(0.9x\lbrack N2O\rbrack)_(\lbrack N2O\rbrack_0)(d\lbrack N2O\rbrack)/(\lbrack N2O\rbrack^2)\text{ = k }\int ^t_0\text{dt }`

-1/2 and k goes out of the integral because they don't change.

We integrate and then we replace the values from the top and the bottom of the integrals

`\int (1)/(x^2)dx\text{ = -}(1)/(x)\text{ + Constant}`
`-(1)/(2)\text{ ( }(1)/(\lbrack N2O\rbrack_0)-\frac{1}{0.9\text{ x}\lbrack N2O\rbrack_0})\text{ = k x t}`
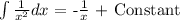
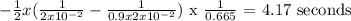
`-(1)/(2)x((1)/(2x10^(-2))-(1)/(0.9x2x10^(-2)))\text{ x }(1)/(0.665)\text{ = 4.17 seconds}`

t = 4.17 s

`\begin{gathered} -(1)/(2)\text{ x ( ) = }\frac{-1\text{ x ( )}}{2}\text{ = k x t ! }\frac{-1\text{ x ( )}}{2\text{ x k}}\text{ }=\text{ t or }(-1)/(2)x\text{ ( ) x }(1)/(k) \\ \\ \\ \end{gathered}`