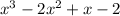Answer:
The required polynomial is
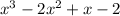
Step-by-step explanation:
Given : A polynomial equation of degree 3 such that two of its roots are 2 and an imaginary number.
To find : The equation of polynomial with degree 3.
Solution :
It is given that the equation has 3 roots one is 2 and othe is imaginary.
So, one root 2 = (x-2)
Let the other two roots are imaginary i, -i
⇒ (x-i),(x+i)
Therefore, the roots of the polynomial of degree 3
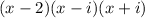
Now, we solve the roots to find the equation,
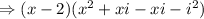
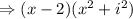
![[i^2=-1]](https://img.qammunity.org/2018/formulas/mathematics/college/z2dbmeq50nlq42q60x0lkcr4d8rmljpw6b.png)
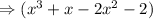
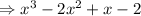
Therefore, the required polynomial is