Question

Write a compound interest function to model the following situation. Then, find the balance after the given number of years.

$17,400 invested at a rate of 2.5% compounded annually; 8 years

Answer 1

y=17400(1+0.025)^8 is your equation and with that you get $21200.21

Answer 2

Compound interest function,
`A = P(1 + (r)/(n) )^(nt)`

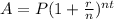
The amount when compounded annually after 8 years is $
`21200.21`

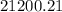
Explanation:

Topic: Compound Interest

To model the situation, we'll make use of the compound interest formula. The formula is as follows:

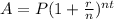`A = P(1 + (r)/(n) )^(nt)` ---- This is the compound interest function

Where

r = Rate = 2.5% = 0.025

n = Period = Annually = 1

t = Time = 8 years

P = Principal Amount = $17,400

A = Amount ---- This is the function we want to model

By Substitution, we have

`A = 17,400(1 + (0.025)/(1) )^(1*8)`

`A = 17,400(1 + 0.025)^(8)`

`A = 17,400(1.025)^(8)`

`A = 17400 * 1.21840289751`

`A = 21200.2104167`

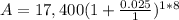
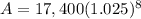
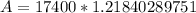
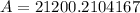
Hence, the amount when compounded annually after 8 years is $
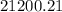`21200.21` (Approximated)