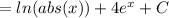Given the integral:
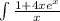
You can evaluate it as follows:
1. Separate it into two integrals with the same denominator:
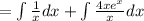
2. Write the constants outside the integral:
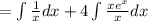
3. Since:
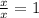
You can keep simplifying:
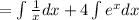
4. Integrate by applying these Integration Rules:
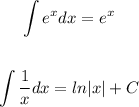
You get:
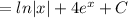
Hence, the answer is:
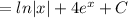
Or: