Question

The drug Valium is eliminated from the bloodstream exponentially with a half-life of 36 hours. Suppose that a patient receives an initial dose of 30 milligrams of Valium at midnight.A) how much Valium is in the patient’s blood at noon on the first day? B) Estimate when the Valium concentration will reach 20% of its initial level.

Answer 1

The formula for calculating half-life is as shown below

`N(t)=N_0((1)/(2))^{(t)/(t2)}`

Where:

`\begin{gathered} N(t)=quantity\text{ of the substance remaining} \\ N_0=initial\text{ quantity of the substance} \\ t=time\text{ elapsed} \\ t_{(1)/(2)}=half\text{ life of the substance} \end{gathered}`

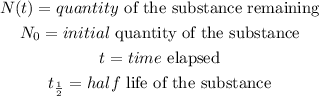
Given that

`\begin{gathered} N(t)=\text{?} \\ N_0=30\text{milligrams} \\ t=12\text{hours} \\ t_{(1)/(2)}=36\text{hours} \end{gathered}`

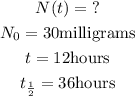
So,

`\begin{gathered} N(t)=30((1)/(2))^{(12)/(36)} \\ N(t)=30((1)/(2))^{(1)/(3)} \\ N(t)=30*0.7937 \\ N(t)=23.811 \\ N(t)=23.8(\text{nearest tenth)} \end{gathered}`

Hence, there is approximately 23.8 milligrams of Valium in the patient's blood at noon on the first day.

B. To estimate when the Valium concentration will reach 20% of its initial level, it is observed that

`\begin{gathered} N(t)=20\text{ \% of }N_0,N_0=30 \\ \\ N(t)=(20)/(100)*30 \\ N(t)=0.2*30=6 \end{gathered}`

Let us substitute into the formula to get t as shown below:

`\begin{gathered} N(t)=N_0((1)/(2))^{(t)/(36)} \\ 6=30_{}(0.5)^{(t)/(36)} \\ (6)/(30)=(0.5)^{(t)/(36)} \\ 0.2=0.5^{(t)/(36)} \\ ^{} \end{gathered}`
`\begin{gathered} In0.2=(t)/(36)In0.5 \\ t=(36In0.2)/(In0.5) \\ t=(36*-1.6094)/(-0.6931) \\ t=83.5894hours \end{gathered}`

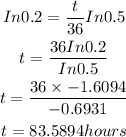
Hence, the valium concentration will reach 205 of its initial level at 83.6 hours