Question

A dairy farmer wants to mix a 75% protein supplement and a standard 25% protein ration to make 1800 pounds of a high-grade 70% protein ration. How many pounds of each should he use?

Answer 1

Step-by-step explanation:

We are given the following;

A farmer wants to make a 70% protein ration

The mix would have;

75% protein supplement

25% protein ration

1800 pounds mix of 70% protein ration

From these details we can make out the following;

`\begin{gathered} Supplement=75\%\text{ of x pounds} \\ \text{Ration}=25\%\text{ of (}1800-x)pounds \\ \text{Mixture}=70\%\text{ of }1800\text{ pounds} \end{gathered}`

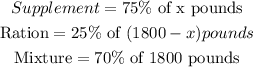
Take note that the mixture would be made up of protein supplements and protein rations. Hence, the total mix of 1800 pounds would be'

Supplements + Ration = Mixture

Where Supplements is x pounds, then Ration would be 1800 minus x to derive the total weight of Ration.

We can now simplify the equations we came up with and we'll have;

`\begin{gathered} 75x+(25\lbrack1800-x\rbrack)=70*1800 \\ 75x+(45000-25x)=126000 \\ 75x+45000-25x=126000 \end{gathered}`
`\begin{gathered} 75x-25x=126000-45000 \\ 50x=81000 \end{gathered}`

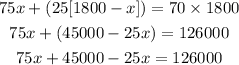
Divide both sides by 50;

`\begin{gathered} (50x)/(50)=(81000)/(50) \\ x=1620 \end{gathered}`

Therefore, for the protein supplement we would have;

`\begin{gathered} 75\%\text{ of 1620}=0.75*1620 \\ =1215 \end{gathered}`

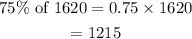
Also, for the protein ration;

`\begin{gathered} \text{Mixture}=\text{Supplement}+\text{Ration} \\ 1800=1215+\text{Ration} \\ 1800-1215=\text{Ration} \\ 585=Ration \end{gathered}`

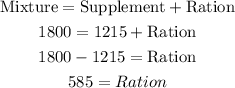
ANSWER:

Protein Supplement = 1215 pounds

Protein Ration = 585 pounds