Question

StepThe logo shown is symmetrical about one of its diagonals. Enter the angle measures in the green triangle,to the nearest degree. (Hint: First find an angle in a blue triangle.) Then, enter the area of the greentriangle, without first entering the areas of the blue triangles. Round your area to the nearest tenth.А4 mmB2 mm2 mmDThe measure of ZCAE isThe measure of ZAEC isThe measure of ZACE isThe area of the green triangle ismma

Answer 1

In order to find the interior angles of the green triangle, first let's find the angle CAB in the upper blue triangle, using its tangent relation:

`\begin{gathered} \tan (\text{CAB})=(2)/(4)=(1)/(2) \\ \text{CAB}=\tan ^(-1)((1)/(2)) \\ \text{CAB}=26.565\degree \end{gathered}`

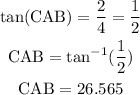
Since the figure is symmetrical, angle FAE is also 26.565° and triangle AEC is isosceles.

Now, we can find angle CAE:

`\begin{gathered} CAE+\text{CAB}+\text{FAE}=90 \\ CAE+26.565+26.565=90 \\ CAE+53.13=90 \\ CAE=36.87\degree \end{gathered}`

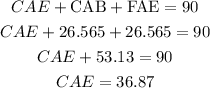
Finding angles ECA and AEC:

`\begin{gathered} ACE+\text{AEC}+CAE=180 \\ ACE+ACE+36.87=180 \\ 2ACE=143.13 \\ ACE=71.565\degree \\ \\ \text{AEC}=ACE \\ \text{AEC}=71.565\degree \end{gathered}`

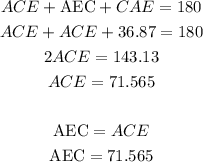
In order to calculate the area of green triangle, we can first calculate the length of all three sides using Pythagorean theorem:

`\begin{gathered} AC^2=AB^2+BC^2 \\ AC^2=16+4 \\ AC^2=20 \\ AC=4.47 \\ \\ AE=AC=4.47 \\ \\ EC^2=ED^2+DC^2 \\ EC^2=4+4 \\ EC^2=8 \\ EC=2.83 \end{gathered}`

So the area of the triangle using Heron's formula is:

`\begin{gathered} A=\sqrt[]{p(p-a)(p-b)(p-c)} \\ p=(4.47+4.47+2.83)/(2)=5.885 \\ A=\sqrt[]{5.885(1.415)\mleft(1.415\mright)\mleft(3.055\mright)} \\ A=6 \end{gathered}`

So the area of the triangle 6 mm².