To find what they ask for we need to find the value of cos x. To do this we need to use the pythagorean identity:
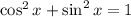
Plugging the value of sine given we have:
![\begin{gathered} \cos ^2x+((4)/(5))^2=1 \\ \cos ^2x+(16)/(25)=1 \\ \cos ^2x=1-(16)/(25) \\ \cos ^2x=(9)/(25) \\ \cos x=\pm\sqrt[]{(9)/(25)} \\ \cos x=\pm(3)/(5) \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/i158s7kyngipbhamx8b1.png)
Now we need to determine the sign of the cosine functions. Since the angle is the first quadrant that means that the cosine should be positive (all the trigonometric functions are positive in the first quadrant). Hence:
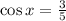
Now that we have the value of the cosine we need to use the identity:
![\cos ((x)/(2))=\pm\sqrt[]{(1+\cos x)/(2)}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/j0p899k8ge7tlw4cv9mh.png)
Once again we need to define the sign of the functions, but we know that the angle x is in the first quadrant, then its half is also in the first quadrant and this implies that the cosine is positve, then we need to use:
![\cos ((x)/(2))=\sqrt[]{(1+\cos x)/(2)}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/fo35e3v1tvr9axl5suge.png)
Plugging the value of the cosine we have:
![\begin{gathered} \cos ((x)/(2))=\sqrt[]{(1+(3)/(5))/(2)} \\ =\sqrt[]{((8)/(5))/(2)} \\ =\sqrt[]{(4)/(5)} \\ =\frac{2}{\sqrt[]{5}} \\ =\frac{2\sqrt[]{5}}{5} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/unrt9xy3i3z6g38i9us8.png)
Therefore:
![\cos ((x)/(2))=\frac{2\sqrt[]{5}}{5}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/ag1dw78hstsaua9femdz.png)