Answer:
Sum of the geometric sequence is 19662.
Explanation:
Sum of the terms in a geometric series is represented by the formula
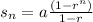
In this formula a = first term
r = common ratio
n = number of terms
Given in the question
a = 6
r = (-4)
n = 7
![S_(7)=(6)([1-(-4)^(7)] )/([1-(-4)])=6.((1+16384))/((1+4))=((6)(16385))/(5)= 19662](https://img.qammunity.org/2018/formulas/mathematics/high-school/fugto7si950daxuvwcnhgl56zso7npvron.png)
Therefore sum of the sequence is 19662