Question

there are 6 people in the ballot for regional judges. voters can vote for any 4. voters can choose to vote for 0,1,2,3,or 4 judges. I'm how many different ways can a person vote?

Answer 1

In 360 different ways can a person vote.

Explanation:

Total numbers of vote one can cast = 4

Number of individuals in ballot = 6

Number of distinct ways are there to form the teams for the class:

`P^(n)_(k)=(n!)/((n-k)!)`

where = n = number of elements = n = 6

k = number of elements choose = 4

`P^(6)_(4)=(6!)/((6-4)!)=360`

In 360 different ways can a person vote.

Answer 2

In 517 ways

Explanation:

There are total 6 people in ballot and voters can vote for any 4 we have following choices

Voter may not vote for anyone then
`^6P_0`

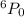
Since,
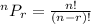`^nP_r=(n!)/((n-r)!)` and
`n!=n(n-1)....1`

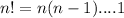
Here, n=6 and r=0 we will get

`^6P_0=(6!)/((6-0)!)=(6!)/(6!)=1`

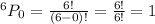
Voter may not vote for one of them then
`^6P_1`

`^6P_1=(6!)/((6-1)!)=(6!)/(5!)=6`

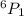
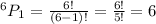
Voter may not vote for two of them then
`^6P_2`

`^6P_2=(6!)/((6-2)!)=(6!)/(4!)=30`

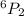
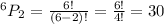
Voter may not vote for three of them then
`^6P_3`

`^6P_3=(6!)/((6-3)!)=(6!)/(3!)=120`

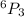
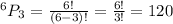
Voter may not vote for four of them then
`^6P_4`

`^6P_4=(6!)/((6-4)!)=(6!)/(2!)=360`

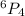
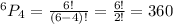
Total ways in which a person can vote is

`^6P_0`+
`^6P_1`+
`^6P_2`+
`^6P_3`+
`^6P_4`

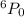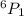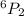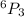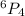
Substituting the values we will get

[tex]1+6+30+120+360=517[/text] ways.