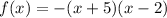Question

F (x) = 10 – 3x – 22*This can be factored using the quadratic formula

Answer 1

You have to factor the following function

`f(x)=10-3x-x^2`

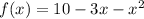
The coefficients of the function are:

a=-1

b=-3

c=10

Using the quadratic formula you have to calculate the roots of the function

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

Replace the formula with the values of the coefficients of the function

`\begin{gathered} x=\frac{-(-3)\pm\sqrt[]{(-3)^2-4(-1)10}}{2(-1)} \\ x=\frac{3\pm\sqrt[]{9+40}}{-2} \\ x=\frac{3\pm\sqrt[]{49}}{-2} \\ x=(3\pm7)/(-2) \end{gathered}`

Positive calculation:

`\begin{gathered} x=(3+7)/(-2) \\ x=(-10)/(-2) \\ x=-5 \end{gathered}`

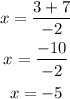
Negative calculation

`\begin{gathered} x=(3-7)/(-2) \\ x=(-4)/(-2) \\ x=2 \end{gathered}`

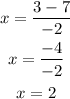
The roots of the function are x=-5 and x=2

The factorized function is

`f(x)=(x+5)(x-2)`

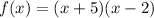
Note that the roots have to have the inverse sign when you write the factorized function.

The final step is to multiply the function by -1, to make it point downwards just like the original one.

`f(x)=-(x+5)(x-2)`