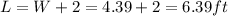Question

The area of a rectangular book shelf is 28 square feet.The length is 2 feet longer than the width.What are the dimensions of the book shelf to the nearest tenth? DRAW DIAGRAM.

Answer 1

Dimensions: W = 4.39 ft; L = 6.39 ft

(a) See explanation

(b) 0 = W² + 2W - 28

(c) W = 4.39 ft

Step-by-step explanation

(a)

(b) We know that the length is 2 feet longer than the width of the shelf,

`L=W+2`

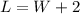
And the area, which is the product of the width and the length is 28ft²,

`28=L\cdot W`

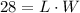
Replace the first equation into the second,

`28=(W+2)W`

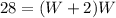
This is a quadratic equation. We can rewrite it in standard form,

`28=W^2+2W`
`0=W^2+2W-28`

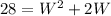
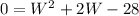
(c) To solve this equation we can use the quadratic formula,

`\begin{gathered} 0=ax^2+bx+c \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \end{gathered}`

In our equation, a = 1, b = 2 and c = -28,

`W=\frac{-2\pm\sqrt[]{2^2-4\cdot1\cdot(-28)}}{2\cdot1}`
`W=\frac{-2\pm\sqrt[]{4+112}}{2}`
`W=\frac{-2\pm\sqrt[]{116}}{2}\approx(-2\pm10.77)/(2)`

One of the results is negative, so we will discard it - a width cannot be negative. We have to use the result with the sum,

`W=(-2+10.77)/(2)=4.39`

The width of the shelf is 4.39 feet, rounded to the nearest hundredth.

Then, we just have to replace W into the first equation to find the length of the shelf,

`L=W+2=4.39+2=6.39ft`