Question

The velocity of a particle moving along the x-axis is v(t) = t2 + 2t + 1, with t measured in minutes and v(t) measured in feet per minute. To the nearest foot find the total distance travelled by the particle from t = 0 to t = 2 minutes.

Answer 1

v(t)=t^2+2t+1 integrating we get d(t)

d(t)=t^3/3+t^2+t or more neatly

d(t)=(t^3+3t^2+3t)/3 so

d(2)=(8+12+6)/3

d(2)=26/3

So the particle moves 9 feet (to the nearest foot) in the first two minutes.

Answer 2

we need to find where the velocity cross the x axis because integrating will only find the displacement

solve
v(t)=0=t^2+2t+1
(t+1)^2
at t=-1
so not in tthe range

so find the area under the curve of v(t) from t=0 to t=2


`\int\limits^2_0 {t^2+2t+1} \, dt`=
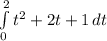
using the reverse power rule

`[ (1)/(3)t^3+t^2+t ]^2_0`=

`(8)/(3) +4+2-0`=

`(8)/(3) + (18)/(3)`=

`(26)/(3)`=
8.666666666666ft
about 9ft