Question

Question 1) How does the binary number 1011001 become 25 in decimal?Question 2) How does decimal number 47 become 101111 in binary?

Answer 1

(1) To convert a binary number to decimal (that is base 10 number), you follow the steps shown below;

`\begin{gathered} (1*2^6)+(0*2^5)+(1*2^4)+(1*2^3)+(0*2^2)+(0*2^1)+(1*2^0) \\ =(64)+(0)+(16)+(8)+(0)+(0)+(1) \\ =89 \end{gathered}`

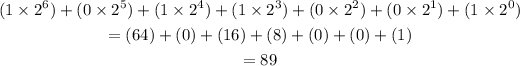
The binary number 1011001 becomes 89 in decimal and NOT 25

(2) To convert a decimal number to a binary number (that is base 2 number), follow the steps shown below;

`\begin{gathered} (47)/(2)=23\text{ (Remainder 1)} \\ (23)/(2)=11\text{ (Remainder 1)} \\ (11)/(2)=5\text{ (Remainder 1)} \\ (5)/(2)=2\text{ (Remainder 1)} \\ (2)/(2)=1\text{ (Remainder 0)} \\ (1)/(2)=0\text{ (Remainder 1)} \\ \text{Next step, you take all the REMAINDERS one after the other} \\ \text{Starting from bottom to the top}.\text{ That now gives you;} \\ 101111_2 \end{gathered}`

So basically, to convert a binary number to a decimal number, you take the digits one after the other and multiply each by 2, and while doing that, express each term as an exponent of the number of digits (starting from the least to zero). That means when you have 7 digits, the first would be "times 2 raised to the power of 6" and so on till you get to the last one which would be "times 2 raised to the power of 0).

Also to convert a decimal number to base 2 OR binary number, you begin to divide the number by 2, and write down the remainder and keep on with the division process with each new result you've yielded, until you get to a zero result. Next step is to take all the remainders from bottom to top and write it out with the number 2 as a subscript (that is on the bottom right side) as shown in our solution above)